Sợi chỉ vàng hình xoắn ốc không có điểm đầu và cũng không có điểm kết, và cuộc sống cũng có một khoảng thời gian khó khăn như vậy, phải không nào? Bạn có thể chấp nhận rằng không có điểm kết thúc bởi cuộc sống là vậy, nhưng lại luôn khát khao để quay ngược về điểm khởi đầu – Khởi nguồn của mọi sự.
Tự nhiên đã tạo ra dãy Fibonacci thật dài để chạy vòng quanh mọi vấn đề. Có vẻ như Chúa đã nói: “Được rồi, hãy ra ngoài đó và sáng tạo cùng với Sợi chỉ vàng hình xoắn ốc”, trong khi chúng ta thì gào lên: “Chúng con không biết làm thế nào.” Vì vậy, chúng ta đã tạo nên một cái gì đó không phải là Sợi chỉ vàng hình xoắn ốc, nhưng nó cũng giống đến đến mức bạn khó có thể phân biệt được [Hình. 8-4].
Ví dụ: Tỷ lệ phi liên quan đến Tỷ lệ vàng, xấp xỉ bằng 1,6180339. Hãy xem điều gì sẽ xảy ra khi bạn chia từng số trong dãy Fibonacci thành số lớn hơn tiếp theo. Đây là dãy ở cột bên trái: 1, 2,3,5,8,13,21,34,55,89. Trong cột thứ hai, tôi đã chuyển từng dãy số để chúng ta có thể chia số trong cột đầu tiên bằng số trong cột thứ hai (xem cột 3). Lưu ý điều gì sẽ xảy ra khi bạn chia những con số ở cột thứ hai vào những con số trong cột một. Khi chúng ta chia 1 cho 1, chúng ta nhận được 1.0. Bây giờ, 1.0 là bé hơn rất nhiều so với tỷ lệ phi. Nhưng khi chúng ta chuyển sang dòng tiếp theo và lấy 2 chia cho, chúng ta có 2, lớn hơn phi. Khi lấy 3 chia cho 2, chúng ta nhận được 1.5, gần với phi hơn rất nhiều so với 2 phép tính trước đó.
Xem thêm Phương pháp Tự học Thiền: https://kimtuthap.org/tuhocthien-html/
Lấy 5 chia cho 3 sẽ ra 1.6666, gần hơn rất nhiều. 8 chia cho 5 thành 1.60. 13 chia cho 8 bằng 1.625. 21 chia cho 13 bằng 1,.615. 34 chia cho 21 bằng 1.619. 55 chia cho 34 bằng 1.617. 89 chia 50 bằng 1.6181. Ngày càng gần hơn với tỷ lệ phi thực tế. Điều này được gọi là đạt đến giới hạn tiệm cận. Nó không bao giờ có thể đạt đến con số đúng, nhưng bạn sẽ không thể nhận ra sự khác biệt sau một vài lần phân chia. Bạn có thể thấy điều này trong đồ thị trong Hình 8-5.
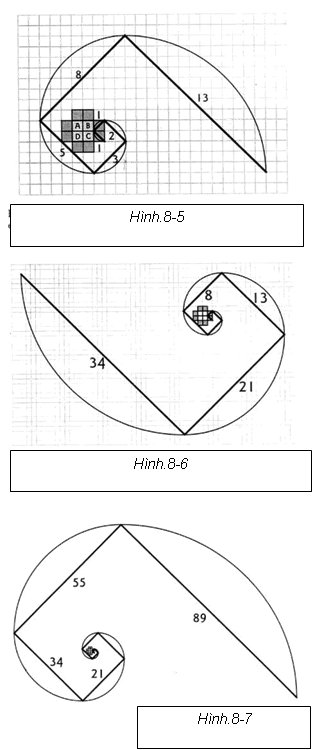Các hình vuông màu xám nhạt là bốn hình vuông trung tâm của cơ thể con người – Nơi chứa tám tế bào đầu tiên. Tám hình vuông màu xám đậm xung quanh những hình vuông trung tâm này là nơi bắt đầu của các đường xoắn ốc.
Thay vì để chúng xoay vòng mãi mãi, chúng ta sẽ làm một điều gì đó khác biệt – Bởi vì đó là cách mà cuộc sống hoạt động. Tôi sẽ sử dụng một trong những hình vuông bên ngoài làm điểm xuất phát, và điều này cũng sẽ áp dụng đúng cho cả tám ô.
Sử dụng một đường chéo chạy qua một trong những hình vuông làm thước đo, chúng ta sẽ gọi đường chéo này là một đơn vị. Sau đó, chúng ta di chuyển theo các số trong dãy Fibonacci: 1, 1, 2,3, 5,8, 13, 21, 34, 89, quay 90 độ sau mỗi con số. Trong bước đầu tiên, chúng ta lấy một đoạn thẳng dài 1 đơn vị, sau đó quay 90 độ và đi thêm một lần nữa. Sau đó, chúng ta quay 90 độ và đi tiếp với đoạn thẳng dài 2 đơn vị, quay thêm 90 độ độ và đi ba đơn vị. Giữa mỗi bước, chúng ta thực hiện quay một góc 90 độ. Bước tiếp theo dài 5 đơn vị, sau đó là 8. Vì vậy, chúng ta có 1,1,2, 3, 5, 8, 13.
Sau đó, chúng ta gạch chéo 21 ô vuông, tiếp đến là 34 [Hình. 8-6]. Rồi 55 và 89 [Hình. 8-7]. Khi chúng ta thực hiện điều này, hình xoắn ốc sẽ được mở rộng và ngày càng gần hơn với tỷ lệ phi, Sợi chỉ vàng hình xoắn ốc, cho đến khi không có cách nào phân biệt được sự khác biệt trong cuộc sống, ít nhất là bằng mắt thường.
So sánh hai hình xoắn ốc phải là một công việc rất quan trọng nếu muốn tìm hiểu về cuộc sống, bởi vì người Ai Cập cổ đại đã biểu diễn cả Fibonacci và Sợi chỉ vàng hình xoắn ốc trong Đại Kim Tự Tháp. Mặc dù các đường xoắn ốc có hai nguồn gốc khác nhau, khi họ đi đến bước 55 và 89, hai đường thẳng dường như giống hệt nhau. Khi những nhà khảo cổ nghiên cứu về Ai Cập nhìn thấy ba kim tự tháp xếp trên đường xoắn ốc, họ nghĩ đó là Sợi chỉ vàng chứ không phải là hình xoắn ốc Fibonacci. Sau đó, họ quay lại và tìm thấy một trong những lỗ hổng. Vài năm sau, họ nhận ra rằng chỉ cách một chút nữa thôi, có thể là một trăm thước hoặc dài hơn, là một điểm được đánh dấu khác. Họ đã không nhận ra là có hai quả cầu. Tôi không biết liệ những nhà khảo cổ đó có hiểu ý nghĩa thật sự của những biểu tượng này không nữa.