Có người gõ cửa. Tôi đã ra mở cửa phòng ngủ và có một anh chàng cao lớn đang đứng đó. Tôi chưa từng gặp anh chàng này trước đây. Anh ta nhìn tôi hơi bẽn lẽn và nói: “Tôi phải đến đây để nói với bạn một số điều. Tôi được phái đến đây bởi Masons để nói với bạn về vòng tròn và hình vuông”.
Điều này khiến tôi giật mình. Tôi như đóng băng lại và nhìn chằm chằm vào anh ấy trong giây lát, cố gắng giải thích mọi điều. Sau đó, tôi nghĩ rằng mình không thật sự quan tâm đến tiến trình, mà là kết quả đang bày ra trước mắt. Tôi nắm lấy tay anh ấy, nói: “Vào đây” rồi đóng cửa lại. Tôi nói: “Có điều gì mà bạn cần phải nói với tôi?” Và rồi anh ấy đã vẽ bản vẽ này (Hình.7-22).
Xem thêm Phương pháp Tự học Thiền: https://kimtuthap.org/tuhocthien-html/
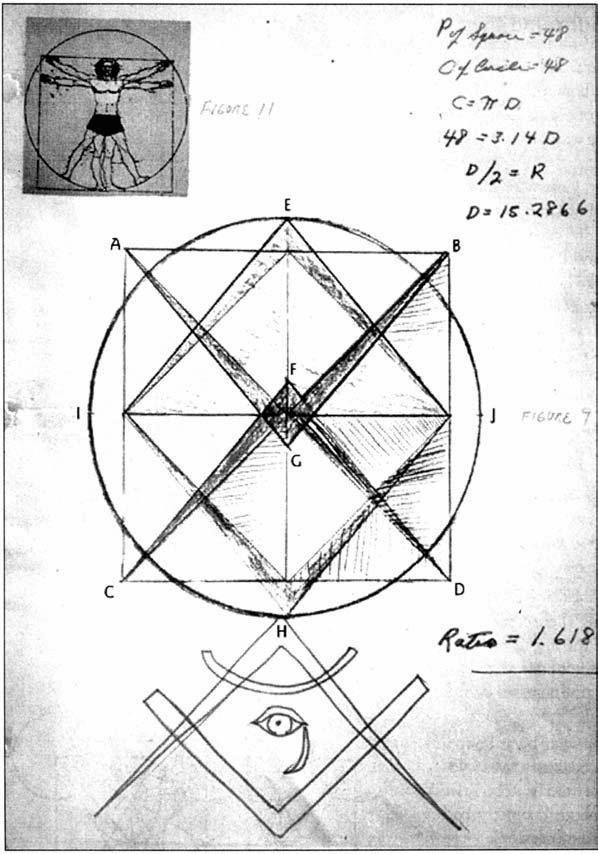
Hình.7-22. Bản vẽ của Mason
Đầu tiên anh ấy vẽ hình vuông, sau đó anh ấy vẽ hình tròn xung quanh hình vuông theo một cách cụ thể – Và nó hiện ra hình ảnh tôi đã thấy phát sáng trong phòng! Anh ta chia hình vuông thành bốn phần, sau đó anh ấy vẽ các đường chéo của hình vuông rồi vẽ các đường chéo qua bốn hình vuông nhỏ hơn. Sau đó, anh ấy vẽ các đường từ I đến E và từ E đến J. Tiếp theo anh ấy vẽ các đường từ I đến H và từ H đến J (E và H là các điểm trên chu vi hình tròn nơi có đường tâm thẳng đứng giao nhau).
Cho đến thời điểm này, tôi không gặp vấn đề gì, nhưng sau đó anh ấy đã vẽ một đường thẳng từ A đến một vị trí nào đó (G) và quay lại B, và từ D đến một vị trí nào đó (F) và quay lại C. Tôi nói: “Chờ một chút, đó không phải là quy luật mà tôi từng được biết. Nó không phù hợp – Không có cơ sở nào cả. Và anh ấy nói: “Không sao, bởi vì đoạn thẳng (A-G) song song với đoạn thẳng (I-H), và đoạn thẳng (D-F) song song với đoạn thẳng (J-E) .
Tôi thốt lên “Đó là một quy luật mới. Tôi chưa từng được biết trước đây. Ý tôi là:. Các đường song song? Được rồi, tôi sẽ lắng nghe tiếp”.
Sau đó anh ấy bắt đầu nói với tôi đủ thứ. Anh ấy nói rằng chìa khóa đầu tiên là chu vi của hình tròn bằng với chu vi của hình vuông – Đó là những gì mà tôi đã nói với bạn trước đây. Hình tròn và hình vuông này cùng là một hình ảnh nhìn từ không trung xuống Đại Kim Tự Tháp với con tàu vũ trụ đáp trên đỉnh.
Tỷ lệ Phi
Anh ấy bắt đầu nói với tôi về tỷ lệ phi: 1,618 (làm tròn thành ba dấu thập phân). Tỷ lệ phi là một mối liên hệ rất đơn giản. Nếu bạn có một cái que và bạn sẽ đánh dấu vào vị trí nào đó, chỉ có hai nơi để đánh dấu tỷ lệ phi, được hiển thị như điểm A và B trong hình minh họa (Hình.7-23).
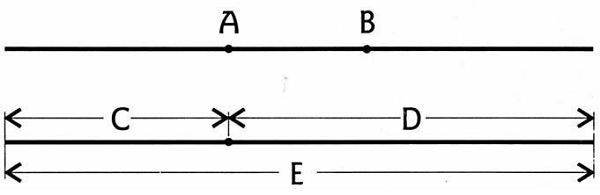
Hình.7-23. Tỷ lệ phi
Chỉ có hai nơi, tùy thuộc vào đỉnh nào. Được thể hiện trên hình vẽ bên dưới, đó là một mối liên hệ: Nếu bạn chia D cho C và E cho D, hai đáp án sẽ giống nhau: 1,618…. Vì vậy, khi bạn chia phần dài hơn cho phần ngắn hơn thì nó sẽ cho bạn tỷ lệ 1,618. Khi chia toàn bộ độ dài của E cho phần ngắn hơn tiếp theo là D thì bạn sẽ có tỷ lệ tương tự. Mặc dù tôi đã học toán ở đại học nhưng bằng một cách nào đó, tôi lại không thể nhớ đến tỷ lệ phi. Tôi phải quay trở lại và học lại tất cả những kiến thức này.
Anh chàng này cũng đưa ra bản vẽ của Leonardo với hình tròn và hình vuông xung quanh nó, cung cấp cho tôi thêm nhiều thông tin hơn. Tôi đã đưa cho anh ấy rấtnhiều câu hỏi, và khoảng một nửa trong số đó anh ấy không biết câu trả lời. Anh ấy chỉ nói rằng: “Đó là cách mà nó hoạt động” hoặc “Tôi không biết; chúng tôi không biết”.
Trước khi rời đi, anh ấy đã vẽ bản phác thảo ở cuối sơ đồ của mình (xem Hình 7-22), với hình vuông và một con mắt phải của ai đó. Sau đó anh ấy rời đi và tôi chưa bao giờ gặp lại anh ấy kể từ thời điểm đó. Tôi thậm chí không nhớ tên của anh ấy nữa.
