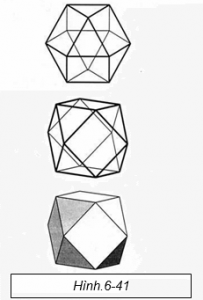
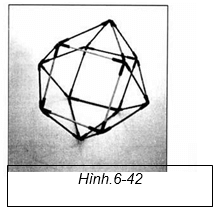
Đây là hình dạng của nó trong không gian ba chiều (Hình.6-41). Nó được gọi là khối lập phương hay vector cân bằng. Bạn có thể thấy rằng ban đầu nó là một khối lập phương, nhưng nếu góc tại điểm A tiếp tục hướng lên trên, nó sẽ tạo thành một khối bát diện. Nó đồng thời là một khối bát diện và một khối lập phương. Nó không còn biết nó là cái gì nữa; nó nằm đâu đó ở khúc giữa. Khi mà Buckminster Fuller tìm thấy khối đa diện này, ông gần như giành trọn thời gian với nó. Ông ấy đã nghĩ rằng khối đa diện này là tối quan trọng, hình dạng vĩ đại nhất từng có trong quá trình sáng tạo, bởi vì nó làm được điều mà không có hình dạng nào khác làm được. Điều đó quan trọng với ông ấy đến nỗi Fuller đã đặt cho nó một cái tên hoàn toàn mới: Vector cân bằng. Ông ấy phát hiện ra rằng hình dạng này, thông qua các mô hình quay khác nhau, trở thành năm khối đa diện đều Platon! Hình dạng này dường như chứa đựng mọi bí mật vĩ đại nhất (Hình.6-42).
Xem thêm Phương pháp Tự học Thiền: https://kimtuthap.org/tuhocthien-html/
Nếu bạn thấy điều này thú vị, hãy mua thứ đồ chơi này [xem phần tham khảo] và chơi với nó. Nó sẽ trả lời tất cả các câu hỏi của bạn nếu bạn cho phép.
Sâu bên trong hạt vừng
Những người khác cũng đã nghiên cứu khối lập phương. Có ai quen với một người tên là Derald Langham không? Không quá nhiều người biết về anh ấy. Anh ấy khá trầm lặng trong cả suốt cuộc đời của mình. Công việc của anh ấy được gọi là Genesa (Nếu bạn muốn nghiên cứu nó) và tôi thật sự tôn trọng người đàn ông này..
Trước hết, anh ấy là một nhà thực vật học đã một tay cứu Nam Mỹ trong Chiến tranh thế giới thứ hai. Họ chết đói, và anh ấy đã tạo ra một loại ngô mọc lên như cỏ dại. Bạn ném nó xuống đất, và nó mọc lên mà hầu như không cần đến nước. Đây quả thật là một món quà tuyệt vời giành cho Lục địa Nam Mỹ. Sau đó, anh ấy nghiên cứu về hạt mè, và khi khám phá sâu bên trong nó, anh ấy đã tìm thấy một khối lập phương. Trong thực tế, khi nhìn sâu vào bên trong của bất kỳ hạt giống nào, bạn sẽ thấy những hình dạng hình học nhỏ được liên kết với các khối đa diện Platon, chủ yếu là khối lập phương.
Derald Langham đã tìm thấy mười ba tia phát ra từ khối lập phương hạt vừng. Tiến hành các nghiên cứu sâu hơn, anh ấy đã phát hiện ra rằng trường năng lượng trong hạt giống cây trồng cũng tồn tại xung quanh cơ thể con người. Nhưng anh ấy tập trung vào khối lập phương, được kết nối với các trường xung quanh cơ thể. Chúng ta sẽ thảo luận điều đó, mặc dù hướng dẫn của tôi tập trung vào một hình dạng khác: Ngôi sao tứ diện. Chúng ta có trường tứ diện sao xung quanh cơ thể, trường này cũng xung quanh hạt, nhưng tạo ra một loạt các quy trình hình học khác với khối lập phương/Vector cân bằng. Langham đã thực hiện một loạt những gì bạn có thể gọi là vũ điệu thiêng liêng (trong cách nói Sufi). Trong đó, bạn di chuyển và kết nối với tất cả các điểm trong trường theo cách mà bạn nhận thức được chúng. Đây thật sự là một thông tin hữu ích.
Hình 6-43 cho thấy một số dạng ba chiều của khối đa diện mà chúng ta đã nói về.
Hình.6-43. Polyhedron
Tại A là khối lập phương mà chúng ta vừa thảo luận; tại B là khối đa diện hình thoi. Cái sau quan trọng vì nó là đối ngẫu của khối lập phương. Nếu bạn nối các tâm của khối lập phương, bạn sẽ có được khối hình thoi và ngược lại. Hình 6-44 cho thấy hình học bên trong của các nguyên tử được phản chiếu như thế nào theo các góc của các tinh thể. Chúng ta đã thấy trước đó, tinh thể ở dạng lập phương, hình bát diện và các dạng khác.
Hình.6-44. So sánh tinh thể