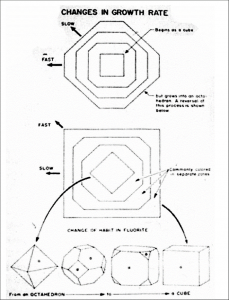
Một cuốn sách địa chất đã cố gắng giải thích sự thay đổi của Fluorite như thế này (Hình.6-36). Ở phía dưới bên phải, bạn thấy một khối lập phương. Bạn có thể cắt bớt bất kỳ hình đa diện nào. Khi thực hiện điều đó (trong trường hợp này là khối lập phương), bạn có thể cắt bỏ các cạnh, các nếp gấp hoặc các mặt. Nếu cắt ngắn khối lập phương này bằng cách cắt các góc một góc 45 độ, bạn sẽ có được hình tiếp theo bên trái. Nếu bạn cắt ngắn nó một lần nữa theo cùng một cách, nó sẽ tạo thành một khối có hình dạng kế tiếp bên trái.
Xem thêm Phương pháp Tự học Thiền: https://kimtuthap.org/tuhocthien-html/
 Hình.6-36. Một tinh thể Fluorite
Hình.6-36. Một tinh thể Fluorite
Nếu bạn làm điều đó một lần nữa, bạn sẽ có một khối hình bát diện (ở ngoài cùng bên trái). Bạn có thể quay lại theo cách khác, cắt bớt các cạnh của khối bát diện, và quay lại toàn bộ quy trình cho đến khi nó trở lại thành một khối lập phương. Đây là nỗ lực của cuốn sách địa chất để giải thích làm thế nào mà Fluorite có thể chuyển đổi hình dạng như vậy. Cuốn sách thật sự chỉ giải thích cách thức mà sự chuyển đổi này có thể xảy ra về mặt hình học.
Nhưng trên thực tế, có một điều còn đáng kinh ngạc hơn nhiều xảy ra khi Fluorite chuyển đổi. Các ion thật sự đã quay và giãn nở hoặc co lại để trở thành một mạng lưới tinh thể khác! Nó phức tạp hơn nhiều so với những gì bạn nhìn thấy trong sách..
Đây là một tinh thể Fluorite khác (Hình.6-37) (Tôi đang sở hữu tinh thể này). Nó rất lớn, khoảng 4 inch trên một cạnh. Bạn không còn thường xuyên được thấy những Fluorite lớn như thế này nữa.
 Hình.6-37. Tinh thể Fluorite của tôi
Hình.6-37. Tinh thể Fluorite của tôi
Ai đó đã đặt cái này trong một cửa sổ – Nơi ánh sáng Mặt Trời chiếu vào viên pha lê, và vì liên kết trong Fluorite rất yếu nên khi ánh sáng Mặt Trời chiếu vào, nó bị nứt dọc theo đường rãnh bát diện.
Ở góc trên bên phải của Hình 6-38 là một khối lập phương. Khối lập phương bên trái đã tự nó cắt ngắn dọc theo các cạnh. Bị cắt bớt hai lần nữa, thứ đáng sợ này đã biến thành một khối tứ diện. Đây là một ví dụ về khối lập phương/khối đa diện trong tinh thể.
 Hình.6-38
Hình.6-38
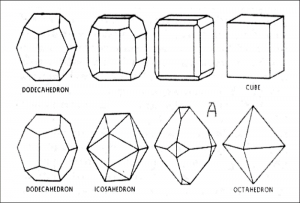
Trong Hình 6-39, tinh thể trên là một khối Pyrite. Nó phát triển theo cách đó, không ai cắt cả. Có một cái khổng lồ như thế này ở Silverado, Colorado, khoảng 6 feet vuông, tôi tin là vậy. Họ chỉ đơn giản là lấy nó ra khỏi lòng đất như một khối lập phương hoàn hảo. Pyrit nhỏ này có hình vuông ở hai đầu, hình chữ nhật ở hai bên. Tinh thể thấp hơn là một Pyrite Dodecahedron tí hon. Một số trong chúng gần như hoàn hảo – Và nó đã phát triển theo cách này ở Peru. Nếu những phiến đá nhỏ này được nằm lại trong lòng đất đủ lâu thì những khối Dodecahedron tí hon đó sẽ biến thành khối lập phương; và thêm một khoảng thời gian nữa, chúng sẽ trở lại thành khối Dodecahedron. Nếu bạn lấy khối Dodecahedron [phía dưới bên trái trong Hình 6-38] và cắt bớt các điểm thì nó biến thành một khối Icosahedron [bên cạnh nó bên phải]. Nếu bạn tiếp tục cắt ngắn các điểm, nó sẽ biến thành một khối bát diện. Tôi có thể tiếp tục công việc cắt ngắn này trong một thời gian dài. Có hàng ngàn cách để làm điều đó. Mỗi một mô hình và một tinh thể, bất kể nó phức tạp đến nhường nào, sẽ biến thành một trong năm khối đa diện Platon nếu bạn cắt ngắn nó vừa đủ, cho thấy bản chất tự nhiên của năm khối đa diện Platon trong cấu trúc tinh thể.
 Hình.6-39
Hình.6-39
Một lưu ý nhỏ: Nếu bạn nhìn vào bên trong một khối tứ diện cắt ngắn làm bằng thủy tinh hoặc pha lê, hoặc thậm chí là gương, nó sẽ phản chiếu ánh sáng. Hình phản chiếu bên trong nó là một khối Icosahedron hoàn hảo. Hãy thử tự mình kiểm tra.
Bạn có thể tiếp tục với điều này. Bạn sẽ thấy một số trông thực sự kỳ lạ, giống như chúng không dựa trên bất kỳ sự Logic nào, nhưng tất cả những gì bạn cần phải có là một chút kiến thức hình học, và bạn sẽ phát hiện ra rằng nó có nguồn gốc từ một trong năm khối đa diện Platon. Không có ngoại lệ. Bất kể mẫu pha lê đó là gì, nó luôn dựa trên khối đa diện Platon. Cấu trúc tinh thể được tạo ra từ Quả sự sống. Nếu muốn xem thêm các tinh thể này, bạn có thể tìm thấy nhiều điều trong Quyển sách Đá và Khoáng sản của Charles A. Sorrell.
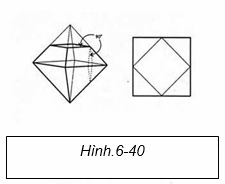
Còn một bộ nữa mà tôi muốn đề cập trở lại. Hình 6-38: “Những khả năng cắt ngắn khác nhau”. Khi bạn cắt một hình bát diện bằng cách cắt tất cả các góc để chúng tạo thành góc 90° (thể hiện tại A trên hình vẽ), nó tạo thành tấm hình như bên trái. Nếu bạn muốn vẽ trên một mặt phẳng, nó sẽ là một hình vuông với một viên kim cương ở giữa (Hình..6-40). Mẫu này tình cờ liên quan đến ý thức của chúng ta, với bản chất tự nhiên của con người.