Đây là một phiên bản thú vị của Bảng tuần hoàn các nguyên tố (Hình.6-47), bởi vì nó cho thấy rằng mọi nguyên tố, với một vài ngoại lệ không thể xác định được vì chúng sẽ không kết tinh, có liên quan đến khối lập phương. Một trong số ít ngoại lệ là Flo, vì Flo hầu như không phản ứng. Nó là một trong những khí trơ nhất. Nhưng trên hầu hết các các nguyên tố khác mà chúng tôi tìm thấy trong mối quan hệ này, ngoại trừ các nguyên tố ở chiều không gian thứ tư nằm ngoài Bảng tuần hoàn của các nguyên tố và những nguyên tố tổng hợp hoặc nhân tạo. Chúng không xảy ra một cách tự nhiên trong tự nhiên.
Xem thêm Phương pháp Tự học Thiền: https://kimtuthap.org/tuhocthien-html/
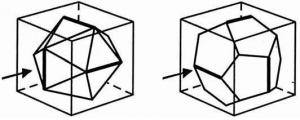
Hình.6-47. Icosahedron và Dodecahedron
Mỗi nguyên tố có một cấu trúc tinh thể liên kết. Trong mọi trường hợp, các nhà khoa học đã tìm thấy rằng các cấu trúc tinh thể khác nhau liên kết với các nguyên tử có thể được thu gọn thành cấu trúc của một hình lập phương. Bạn có thể đã nhận thấy rằng hình lập phương có vẻ quan trọng hơn các đa giác khác. Ví dụ, các tinh thể được chia thành sáu loại khác nhau, nhưng khối lập phương là cơ sở của tất cả chúng. Kinh Thánh nói rằng ngai vàng của Đức Chúa Trời có rất nhiều khối lập phương theo các hướng khác nhau. Khi bạn tạo một cái ngai, nó sẽ là một khối lập phương. Các Pharaoh ở Ai Cập ngồi trên một khối lập phương.
Chìa khóa: Khối lập phương và khối cầu
Khối lập phương khác với những khối đa diện đều Platon khác bởi vì nó có một đặc điểm mà các khối khác không có – Ngoại trừ hình cầu. Cả hình cầu và hình lập phương đều có thể chứa bốn khối còn lại một cách hoàn hảo. Những khối đa diện đều Platon đối xứng với nhau theo bề mặt của chúng nếu bạn có kích thước phù hợp. Khối lập phương là khối đa diện đều Platon duy nhất có đặc tính đặc biệt này: Bạn có thể lấy một quả cầu, luồn nó vào bên trong một khối lập phương, và nó sẽ chạm vào sáu mặt hoàn hảo và đối xứng. Và một ngôi sao tứ diện sẽ trượt xuống một trong các trục và trở thành các đường chéo của khối lập phương, khớp hoàn toàn và đối xứng. Một ngôi sao tứ diện cũng sẽ vừa khít hoàn toàn bên trong một khối lập phương. Bát diện là đối ngẫu của hình lập phương; nếu bạn kết nối các trung tâm của các mặt khối liền kề, bạn sẽ có một khối bát diện. Đối với 2 khối đa diện đều cuối cùng, không giống như là chúng có thể đối xứng với khối lập phương và hình cầu, nhưng thật ra thì chúng hoàn toàn khả khi. Có một chút khó khăn trong việc minh họa, nhưng bạn có thể tự khám phá. Sử dụng một mô hình thực tế, chỉ tìm nơi mà 2 khối Icosahedron và khối Dodecahedron có sáu cạnh trong các mặt phẳng của khối lập phương, và bạn sẽ khám phá ra điều bí mật. Bạn sẽ thấy cách chúng trượt vào các mặt của khối lập phương (Hình.6-48).
Bạn có thể thấy bốn khối đa diện đều Platon khác nằm đối xứng với nhau thành hình lập phương và hình cầu. Điều quan trọng ở đây là chỉ có hình cầu và hình lập phương mới có đặc tính này. Hình lập phương là cha, là hình dạng nam tính quan trọng nhất. Hình cầu là mẹ, là hình dạng nữ tính quan trọng nhất. Vì vậy, trong toàn bộ Thực Tại, hình cầu và hình lập phương là hai hình dạng quan trọng và hầu như sẽ luôn chiếm ưu thế khi nói đến những mối liên hệ nguyên thủy trong sự sáng tạo.
Chính vì lý do này mà một người tên là Walter Russell đã làm một số công việc liên quan đến chủ đề này. Tôi không tin là anh ấy biết bất kỳ điều gì về hình học linh thiêng. Tuy nhiên, anh ấy đã nắm bắt nó bằng trực giác của mình. Và khi những hình ảnh hiện ra trong đầu, anh ấy đã chọn khối lập phương và khối cầu là những mẫu hình học chính để diễn tả về những gì anh ấy đã hiểu. Và bởi vì anh ấy đã chọn hai hình dạng này chứ không phải những khối khác nên Walter có khả năng để đi xa hơn. Nếu như chọn bất kỳ hình dạng nào khác, anh ấy sẽ phạm một sai lầm lớn và sẽ không thể thực hiện được công việc mà mình đã hoàn thành.
Hình.6-48
