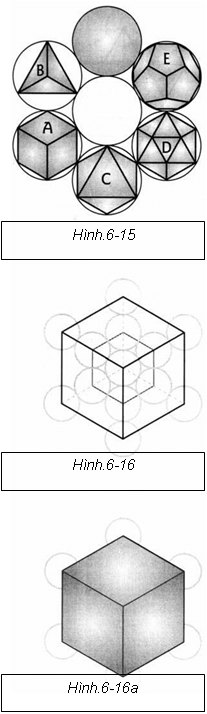
Bất kỳ ai đã nghiên cứu hình học linh thiêng hoặc thậm chí chỉ là hình học thông thường đều biết rằng có năm hình dạng độc đáo, và chúng rất quan trọng để tìm hiểu trong cả hình học linh thiêng lẫn hình học thông thường. Chúng được gọi là những khối đa diện đều Platon (Hình.6-15).
Xem thêm Phương pháp Tự học Thiền: https://kimtuthap.org/tuhocthien-html/
Theo định nghĩa, một khối đa diện đều Platon có những đặc tính đặc trưng. Trước hết, các bề mặt của nó có cùng kích thước. Ví dụ, một khối lập phương, được biết đến nhiều nhất trong số các khối đa diện đều Platon, có một hình vuông trên tất cả các mặt, vì vậy tất cả các mặt đều có cùng kích thước. Thứ hai, các cạnh của khối đa diện đều Platon có cùng chiều dài; tất cả các cạnh của một hình lập phương có cùng chiều dài. Thứ ba, chỉ có một góc giữa các mặt. Trong trường hợp của một khối lập phương, góc này là 90 độ. Và thứ tư, nếu một khối đa diện đều Platon được đặt bên trong một quả cầu (có kích thước phù hợp) thì tất cả các điểm sẽ tiếp xúc với bề mặt của hình cầu. Với định nghĩa đó, chỉ có bốn hình dạng ngoài khối lập phương (A) có tất cả các đặc điểm đó. Thứ hai (B) là tứ diện (tứ diện có nghĩa là bốn mặt), một hình đa diện có bốn mặt, tất cả là tam giác đều, độ dài một cạnh và một góc, và tất cả điểm tiếp xúc với bề mặt của một hình cầu. Hình đơn giản còn lại là (C) một khối bát diện (octa có nghĩa là tám), có tám mặt là tam giác đều có cùng kích thước, độ dài cạnh và góc, và tất cả các điểm chạm vào bề mặt của một quả cầu.
Hai khối đa diện đều Platon khác phức tạp hơn một chút. Một (D) được gọi là khối nhị thập diện, có nghĩa là nó có 20 mặt, được tạo bởi các tam giác đều với cùng độ dài cạnh và góc, và tất cả các điểm tiếp xúc với bề mặt của một hình cầu. Hình cuối cùng (E) được gọi là khối thập nhị (dodeca là 12), có các mặt là 12 ngũ giác (năm cạnh), có cùng độ dài cạnh và góc và các điểm của nó đều tiếp xúc với bề mặt của một hình cầu.
Nếu bạn là một kỹ sư hoặc một kiến trúc sư, bạn đã học năm hình dạng này ở trường đại học, ít nhất là một cách tóm lược, bởi vì chúng là cơ sở của cấu trúc.